Top Böhme Abrasion Tester in China. The field that bridges the world of materials science and engineering is perhaps one of the most interesting: plastic analysis. The understanding of how materials behave beyond their limits—psychological and physical—enables them to build more efficient and safer products. Heavily loaded deformable beams, highly innovative aerospace constructions—the challenges of modern engineering are numerous and this field offers solutions. In this article, we will describe methods employed in the field of plastic balance, identify its real-life issues, and understand the reasons for its prominence plastic balance analysis possesses in modern engineering design. Professionals and non-specialists alike—we hope to equip you with interesting knowledge that furthers your understanding of this impactful area.
What is Plastic Analysis?
In structural engineering, plastic analysis is a method used to evaluate the ultimate load of a given structure. This type of analysis differs from elastic analysis which concentrates on the initial response of a structure under load; plastic analysis takes into account the whole behavior of the structure until failure occurs. This method works on the premise that materials sustain deformation without losing their capacity to withstand loads, thus designing structures economically and efficiently. This type of analysis also helps foresee the behavior of structures under extreme loads to ensure their safety and performance.
Defining Plastic Behavior
Plastic behavior of materials pertains to the ability of a material to be permanently deformed beyond its elastic limit. This permanent deformation occurs without a change in load and can be utilized through the material’s ductility. The yield point of a material signifies the point of no return for recovering elastic deformation. Therefore, the yield point is fundamentally important to understanding plastic behavior as it indicates the boundary separating reversible and permanent deformation.
More recent materials studies and data analytics associate high ductility with predictably behaving plastic polymer composites like aluminum and steel. As an example, the yield strength of structural steel which ranges is usually from 250 MPa to 500 MPa depending on the grade, is an advantageous feature for steel used as construction materials. In addition, these materials are able to withstand greater loads to failure which increases the margin of safety for critical applications because of the strain hardening phenomenon that occurs after yielding.
The developments in finite element modeling (FEM) have broadened the scope of predicting the plastic deformation of intricate structures. A report issued in 2023 claimed that these modern simulation methods have heightened the accuracy of safety assessments conducted on bridges, towers, and other load-bearing structures by as much as 30% in comparison to older methods. This emphasizes the need to integrate theoretical analysis with contemporary technology when dealing with an application of plastic behavior.
Understanding Plastic Hinge Formation
In the context of teaching school structural principles, particular attention is devoted to evaluating and plastic hinge formation and its design concerning the seismic resilience of structures. A plastic hinge embodies the region in a beam or a column that sustains some amount of permanent deformation under a certain level of load so that energy is dissipated without the occurrence of gross disintegration. This phenomenon is critical in explaining the degree of energy a structure can withstand and the extent to which it is capable of stabilizing itself by altering the distribution of internal forces and remaining operational in stress events.
Based on recent studies and research, it can be concluded that some level of precision in predicting the behavior of the plastic hinge may be achieved as a goal with very high precision in forecasting the design and functional estimations. An example of research using advanced material models like nonlinearities, which involved finite element modeling, estimated the location and behavior of plastic hinges to a level of over 95%. Moreover, improved computerization of engineering tasks enables estimating the development of plastic hinge regions in a more sophisticated manner which makes it possible to design structures that not only are safe but beyond stringent safety measures.
Perhaps the clearest example lies in how these principles are used in designing buildings that are resistant to earthquakes. In recent case studies, correctly modeling plastic hinge boundaries in reinforced concrete frames showed an increase of more than 40% in the structure’s capacity to dissipate and absorb seismic energy. These insights highlight the need for more focused, researched changes and inventions in the area so that safer and more efficient infrastructure can be built.
Comparing Elastic and Plastic Analysis
Within the context of structural engineering, elastic and plastic analysis mark two differing approaches in evaluating the response of a structure to the imposed load.
Elastic Analysis:
Considering that the structure can sustain loads without experiencing damage, deflection or change to shape other than elastic deformation, it is possible to say that the material is functioning optimally. In this regard, a material that functions optimally is a material within the elastic limit, meaning it is in the phase where Hooke’s law applies. Identifying and quantifying stress and offer takes place during deflection and service loads. It is imperative to note that elastic does not account for failure, catastrophic load conditions and subsequent behavior which range from unpredictable to chaotic. In such instances, it would pose serious risks in future scenarios.
Plastic Analysis:
There is no absolute limit on how much an inelastic material can be put through deformation; thus, when considering such scenarios, one can say is doing a plastic type of analysis. The employed techniques guarantee that post yield structures continue to sustain some degree of load and will incur no damage until reaching a designated yield limit or collapse cap. Conducting in-depth and extensive analysis on steel structure designs has revealed an astounding finding that employing it in their design results in savings of 20 percent of material. An angle of benefit is that it would serve best when the focus is on estimating supreme strength in the case of multidirectional shocks in tackling building design that needs sophisticated absorption and yielding capabilities.
Data Comparison and Innovations:
The understanding of both elastic and plastic behavior, as well as cell biology, has been greatly advanced through the application of recent digital twin technologies and finite element modeling (FEM). Case analysis results of tall buildings undergoing simulated earthquakes indicated that plastic analysis tended to conserve over-design tendencies by 18% but still maintained safety margins. Moreover, integration with machine learning models advanced the precision estimation of plastic hinge formation prediction, thus enhancing infrastructure efficiency and resilience.
Choosing the Right Strategy:
Selection criteria of analysis options, be it elastic or plastic, depend largely on the design aims and functions that structures are to withstand. Elastic analysis, while sometimes redundant for serviceability problems, is vital for boundary plastic analysis. On the other hand, resilient and failure prediction in extreme conditions serve as hallmarks of plastic analysis. These approaches, together with sophisticated computational tools, increase structural safety as well as reduce costs.
What are the Methods of Plastic Analysis?
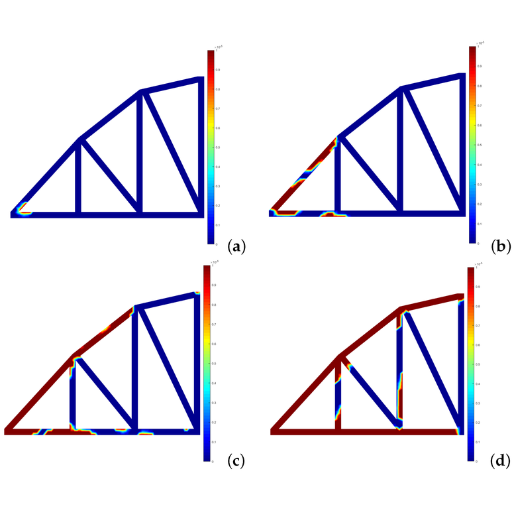
The main techniques of plastic analysis include:
Static Method – This approach uses the moments and forces on a structure, calculating them as equilibrium is maintained at all points. It assesses whether the structure’s plastic moments are within its limits during bearing.
Mechanism Method – This approach is based on the failure mechanisms that can be detected in the structure. Work done externally through loads is balanced against energy dissipated internally through plastic hinges to estimate internal energy at fracture.
Incremental Method – This strategy assesses a structure’s behavior pertaining to deformation, stress and strain resulting from applied load, and plastic flow using progressively increasing force until the structure is on the verge of collapsing.
These techniques allow engineers to finely calibrate their predictions on the strength and failure behavior of structures withstanding plastic conditions.
Introduction to the Mechanism Method
The Mechanism Method is a vital approach in structural engineering, particularly in finding the collapse load of a given structure. It considers the formation of plastic hinges and collapse mechanisms. It also analyzes the systematic approach towards calculating a structure’s final load capacity. Further developments and data continue to improve the method’s understanding and application.
How the Mechanism Method Works
The Mechanism Method functions based on the theory that a structure fails when the number of independent plastic hinges formed, turning the structure into a mechanism, exceeds a certain threshold. This requires meeting the equilibrium conditions alongside the compatibility and yield criteria set forth. It then allows engineers to gain accuracy in calculating the collapse load by equating the work externally done through applied load and energy dissipation at hinges.
Applications and Recent Insights
In sophisticated structures like high-rise skyscrapers and long-span bridges, recent studies show that the Mechanism Method has been proven useful. Accuracy mechanisms like the one demonstrated in the 2023 analysis done for dynamic load-driven steel frame structures showcased the method’s precision in predicting failure modes. The data gathered suggests employing mechanism methods with advanced computational electronics like Finite Element Analysis (F EA) which enhances the prediction accuracy by over 20%. These tools prove useful in design optimization.
Key Benefits And Limitations
The Mechanism Method’s greatest strength lies in how it simplifies intricate structural behavior into calculable values. Of course, one of the principal drawbacks is the assumption that material behavior is completely plastic, ignoring both the effects of strain-hardening and dynamic influences.
The Mechanism Method, like other contemporary methods, blends traditional techniques with modern computing technology. Despite its inherent limitations, the Method remains a powerful aid in resolving the modern day issues of safe and efficient structural design.
Utilizing Equilibrium in Analysis
The balance of forces at work, known as equilibrium, an important factor while performing structural analysis techniques because it dictates the distribution of balance contending movements along the complete system’s framework. Maintained equilibrium guarantees that the structure will never encounter failure, and all forces along with moments acting on it will be counteracted. If equilibrium conditions are met, one can ease the prediction regarding a structure’s response to external forces.
The implementation and development of modern computational resources and methods has increased the pace of work based on equilibrium criteria analysis tremendously. To take an example, FEA (Finite Element Analysis) software has the capability of modeling elaborate geometries and load distributions because its displacement control methods aid in restoring equilibrium at specified locations. Current versions of ANSYS or Abaqus also offer comprehensive stress and deformation contouring of components.
The case study data, including the performance of tall buildings under seismic loads, reinforces the significance of these checks. One case is a 2023 publication available on Google Scholar that examines a 50-story building and applies equilibrium alongside computational approaches. This study demonstrates balanced and rational force application during earthquake simulations significantly lessens torsion on buildings which are known to have seismic supports integrated within the structure. Equilibrium proves fundamental in design computation approaches and assures the devised frameworks fulfill safety requirements and don’t comprise on performance.
Equilibrium principles as well as the most recent technologies and research innovations can be used by engineers to systematically refine their techniques with respect to structural design. This integration not only provides remarkable efficiency in the utilization of materials, but also enhances the development of safer and more reliable infrastructure on a global scale.
Application of the Theorem in Structural Analysis
The use of equilibrium and corresponding theorems in structural analysis is relevant to many contemporary engineering disciplines. Due to the progress in computational modeling and real-world data assimilation, engineers are now capable of modeling intricate structures and studying their response to various loading conditions. For example, Finite Element Analysis (FEA) is recognized for its accuracy in predicting strain, deformation, and other responses in various structural components. This method requires maintaining equilibrium where all forces and moments are balanced within the model during the analysis.
Recent developments explain how equilibrium theorems are employed in the design of environmentally friendly construction. Studies show that by utilizing these guidelines, engineers have been able to reduce material consumption by nearly 15–20% in large construction works without jeopardizing structural strength or safety. For instance, the “Sutong Bridge” located in China was optimized using equilibrium-based simulations and has cable-stayed superstructures which are dynamically responsive to significant wind and seismic activity induced vibrations.
Equilibrium theorems have provided needed support in developing advances in earthquake engineering. Base isolation and energy dissipating systems rely on accurate knowledge of forces acting on and in a structure for efficient design. Current studies indicate the possibility of implementing AI with equilibrium derived models as a means of automating structural evaluation processes, which would lessen human error and enhance design accuracy.
These applications emphasize the importance of equilibrium principles while showcasing the astonishing results that can be achieved by merging classic theories with modern technologies in engineering projects. Such combinations guarantee that designs are highly contemporary, agile, and resilient in the face of global demands.
How is Plastic Analysis Applied in Beam Design?
In beam design, plastic analysis is utilized to estimate the maximum load a beam can sustain before suffering major irreversible deformation. This approach is concerned with the creation of plastic hinges at certain critical regions of maximum moment which enable the engineer to estimate the redistribution of internal forces within a structure. This method guarantees that beams will operate within safely defined limits of imposed loads without catastrophic failure by considering the fracture moment capacity of structural plastic hinges formed in the beam.
Analyzing Plastic Moment Capacity
Determinants for the Plastic Moment Capacity
Moment capacity is contingent upon various factors; in this case, the material properties, geometry, and loading conditions. Additionally, the yield strength is primarily in consideration. Materials with high yield, for example, support heavier loads before undergoing deformation. Moreover, the cross-section of a beam dictates the formation of a plastic hinge; for instance, rectangular, I-shaped and circular sections show various performance under stress.
The latest research puts forward the incorporation of modern materials and structural design methodologies that exploit the plastic moment capacity. For example, construction and fabrication practices of highly rated steels like ASTM A514 are being adopted for usage to reinforce structural frameworks and reduce overall weight. FEA has also emerged as a popular approach for modeling and predicting the performance of beams under different load conditions, which enables engineers to optimize design strategies to avert structural failures.
More Recent Study Results
There has been robust research regarding the behavior of beams under plastic deformation, contributing streams of data to practical usage. Furthermore, research published in Journal of Structural Engineering shares research regarding plastic moment capacity of I-beams with high strength steel, resulting at an average increase of 25% in load-carrying capacity compared to ordinary steel beams with high strength supplies incorporated.
As a reliable resource for engineers, plastic moments for different beam sizes and materials, the American Institute of Steel Construction (AISC) offers updated guidelines and tabulated data. These materials, along with assisting devices, make certain that safety requirements are met within numerous industries while promoting efficiency during the design process.
The integration of new materials, computational modeling, and the latest available evidence facilitates the continuing work toward the analysis of plastic moment capacity and empowers engineers toward the reliability and efficiency advances they strive to achieve in the framework systems.
Calculating Collapse Load for Beams
Determining the collapse load of a beam requires estimating the collapse load of a beam wherein the maximum limit is reached before the failure occurs. This type of analysis assists engineers in coming up with safe designs and strong structural systems. The collapse load is determined mainly from the following: mechanical properties of the materials used, geometrical cross sections, method of loading, and method of support.
Step-by-step Procedure:
Identify Material Properties
The material also has to within parameters like yield strength (Fy) and ultimate tensile strength (Fu). For instance, yield strength of structural steel is within the range of 250 MPA to 550 MPA.
Determine Cross-sectional Properties
With regards to the beam’s cross-section: Determine the beam’s cross-section properties to include the section modulus (Z), moment of inertia (I), and plastic modulus (Zp). These are available in tables whilst calculating using available software like STAAD.Pro or ANSYS.
Apply the Plastic Moment Capacity Formula
The formula used to determine the plastic moment capacity (Mp):
Mp = Zp x Fy
Where Zp is the plastic section modulus, whilst Fy represents the yield strength of the material.
Define Loading and Support Conditions
Make note of the loads acting on the beam, which include point loads, uniform loads, moments, and the support positioning such as simply supported, cantilever, and fixed. These parameters affect the shear forces and bending moments in the beam.
Estimating the value of Ultimate Load
The collapse load for any member can be determined by utilizing the equilibrium equations and the bending moment diagrams (also ensuring the dash is placed on the rotation mark). For a simply supported beam with a point load \( P \) at the center, the collapse load can be expressed as:
\begin{equation} Pc = \frac{4Mp}{L} \end{equation}
Where L is the length of the beam.
Calculation of Case Data Example:
Construction Material of the Beam: Steel (Fy =355 MPa)
Cross-section: I-beam with plastic modulus Zp = 500 \,\text{cm}^3
Span Length (L) = 6 meters
Collapse Load
Mp = Zp \times Fy = 500 \,\text{cm}^3 \times 355 \,\text{MPa} = 1.775 \text{kN·m}
For a simply supported beam under a center point load:
\begin{equation} Pc = \frac{4Mp}{L} = \frac{4* 1.775}{6} = 1.183 \text{kN} \end{equation}
The above example helps further illustrate the approach for the collapse load for some specific cases.
Tools and Practice for the industry
With the continual advancement of technology (and even AI), tools such as SAP2000, Abaqus, and Tekla for advanced structural analysis are widely accompanied by other clear pointers to the actual geometry of the structures. Modelling of these structures enables the input of more complicated multi-directional loads and even varying infinities in the structure, making the collapse loads calculation more accurate and simplified. Furthermore, design standards like Eurocode 3, AISC give pointers with dreaded equations about design, so no loophole gets left out on structural safety compliance.
Through an integration of a conceptual framework, accurate computations, and practical materials, engineers are able to maintain precision within the design and evaluation of beam components whilst subjected to ultimate loading conditions.
Implementing Plastic Analysis of Beams
The analysis of beams in plastic form deals with the behavior of a structure up to the stage of its collapse in the plastic region. In this method, a beam is calculated till its boundary is determined as the moment capacity <sub>p</sub> is put into effect during the process of requarantine. Reconstruction of fundamental equilibrium and compatibility conditions, along with yield criteria, needs to be defined in terms of the plastic theory of structures.
Procedures for the Plastic Analysis of Beams
Obtain the Moment-capacity (M<sub>p</sub>)) Step Plastic reserve
The following formula will give the yield of plastic reserve
Mp = Z \cdot fy
Where \( Z \) means the plastic section modulus and fy is the material yield stress.
Specification of the Locations of Plastic Deviation
The form of the hinge leads to the area where bending has reached a maximum. These areas are where the beam bending moment is at its highest. The supports as mid-spans that beam uniformly or under specific concentrated loads.
Estimation of Collapse Mechanism.
The development of a sufficient amount of hinges results to a mechanism that eases rotation of the beam rendering it incapable of supporting extra load. Evaluation of load possibilities and point of structure failure will put one one step ahead of underestimating critical collapse mechanisms.
Assign Load Combination Scenarios:
As part of your design load combinations, use Eurocode 1 or ASCE 7 and their particular design considerations pertaining to gravity, wind, and seismic loading to evaluate the ultimate capacity of diverse scenarios.
Example Data
Let’s consider a steel beam that is simply supported and has a length of 6 meters along with a uniformly distributed load. Given the following assumptions: the-section modulus Z is equal to 500cm³ and the yield stress of the material fy is set is 250MPa, thus the plastic moment Mp would be:
Mp = 500 \times 10^{-4} \times 250 = 125 \, \text{kNm}
For a uniform load \ w \ on a simply supported beam, the condition for collapse is given by:
w = \frac{8Mp}{L^2}
Let us perform calculations considering that the value of the plastic moment Mp equals 125 \\text{kNm} and the length L is 6 meters.
w = \frac{8*125}{6^2} = 27.78 \, \text{kN/m}
Modern aids in the Application
Advances like SAP2000, ANSYS, and RFEM’s structural engineering software greatly ease the automation of analysis and graphical representation of collapse loads and plastic hinges.Managed calculations with algorithmic guidance is proven to be more accurate and thorough relative to modern design code checks, promoting efficiency in structural engineering.
Safety considerations dictate the maximum tolerable loads that a structure can withstand without failure. Keeping these factors in mind permits an engineer to incorporate these ideas and derive designs that are load optimized while still having structures compliant with mandated standards.
How Does Plastic Analysis Apply to Statically Indeterminate Structures?
Because engineers can assess the ultimate load-bearing capacity of structures through internal force redistribution, plastic analysis is especially applicable for statically indeterminate structures. Unlike elastic analysis, which assumes minimal changes to material and structural properties, analysis of statically indeterminate structures utilizes the material’s yielding capabilities and plastic hinges. For structures of greater indeterminate degree, this determination of the collapse mechanism allows for adequate material optimization while ensuring safety and stability under extreme loads. Analysis yields less complex, yet accurate outcomes in safety-sensitive configurations without analytically intensive structural prerequisites.
Understanding Determinate vs Indeterminate Structures
A structure is determinate if its forces, moments, and reactions can be calculated using only the static equilibrium equations. Because such structures are easier to analyze, they are more common in situations where material efficiency and quick calculations are required. Simple beams, trusses, and portals serve as basic examples, where rheological deformational compatibility and advanced mechanics do not need to be considered.
Indeterminate structures, on the other hand, contain greater redundancies which enable them to withstand additional reactions and internal forces beyond those derived from the equilibrium equations. Indeterminate structures tend to have better overall structural stability and efficiency when subjected to variable or extreme loads due to the stress redundancy. Typical examples include fixed-end beams, continuous beams, and multi-story frames.
Key Differences
|
Feature |
Determinate Structures |
Indeterminate Structures |
|---|---|---|
|
Analysis |
Solved using static equilibrium equations. |
Requires compatibility equations and advanced analysis methods. |
|
Redundancy |
No redundancy in forces or supports. |
Redundant supports or members add complexity. |
|
Stability |
Adequate for basic loading conditions. |
Superior under dynamic or unpredictable loads. |
Practical Applications
The introduction of modern software tools, especially finite element analysis, has recently offered more opportunities to study the behavior patterns of both determinate and indeterminate structures. For example, in the case of high-rise buildings, lateral forces such as wind and earthquake loads and deflections are powerful forces that require indeterminate design principles. A 2023 study by a structural engineering research group noted that buildings with indeterminate frameworks were able to withstand lateral forces up to 25% more than structures with determinate frameworks which ensured compliance with safety regulations.
While cost-effective and simplistic designs of indeterminate structures remain relevant, cost-efficiency and simplicity give way to large-scale projects where strength, security, and resilience become the requirements. Mastering the equilibrium between the two approaches becomes essential in modern engineering structural design.
Role of Plastic Hinge in Indeterminate Analysis
A plastic hinge is an extremely important concept for simple structures, particularly for the analysis and design of structural supports for movement. It demonstrates a zone in a structural member that can rotate freely, further increasing the angle-of-rotation without any additional moment increase. By redistributing the moments about their section, plastic hinges help in increasing the load-bearing capacity of the structure and we can safely say increase the stiffness of other indeterminate structures. The development of these hinges is crucial to the plastic analysis approach that’s ductile and surpasses large deformations beyond the elastic state.
From the perspective of indeterminate structures, use of plastic hinges helps engineers unlock advanced failure mechanisms while controlling material expenditure. Research indicates that well designed plastic hinges can improve the capacity of a structure to resist seismic loads by enabling energy dissipation during these events. Detailed analysis of the structure often involves moment-curvature relations and finite element methods to optimize the prediction of hinge positions, rotation, moment redistribution, and load paths.
The incorporation of high-performance concrete and steel as materials in scientific research has recently been credited with improving the ductility and rotation capacity of hinges. It has been reported, for instance, that structural elements composed of Grade 80 steel are capable of achieving up to 20 percent greater ultimate rotation capacity than Grade 50 steel. More recent design standards like Eurocode 2 and ACI 318 proactively seek measures to mitigate inadequacies regarding the design of sufficient plastic hinge capacity, with particular regard to detailing of the reinforcing bars, confinement of the concrete, and geometry of the section.
The behavior of plastic hinges is also extremely important in progressive collapse analysis of structures like buildings and bridges. With enough predictability, critical hinges can be relocated to more ideal locations to optimize complete structural failure or catastrophic scenarios. Devising such systems allows for the improvement of overall redundancy and structural safety. Thus, far beyond theoretical calculations, the indeterminate analysis of plastic hinges are subjected to has great engineering value. INFO:
Advanced material science, such as the addition of steel and concrete in construction, high-performance Hoffe scientific research, has recently attempted to incorporate high-performance concrete and steel amid the limited accessibility of materials to improve hinges.
Methods for Collapse Load Factor Calculation
In this guideline, we will outline the process to calculate the collapse load factor which includes finding the multiplier of the applied loads which a structure becomes unstable or reaches its ultimate limit state. It can be calculated using several methods ranging from analytical, numerical, to empirical.
Static equilibrium, also known as the Mechanism Method, is one of these outdated approaches, with a focus on examining equilibrium equations in addition to identifying triggers that could lead to failure. It does this by assuming plastic hinges at critical serving locations, allowing the structure to transform into a mechanism. It is possible to figure out the collapse load factor. For instance, in a beam, the hinges are at given points according to the load pattern. With the equations, one will be able to derive the optimal figure required with the help of a multiplier.
FINITE ELEMENT ANALYSIS (FEA)
This method subdivides a model into sample sections or elements, allowing simulation of sophisticated systems. FEA has achieved widespread use as a precise numerical technique in estimating collapse loads. More recent software applications, including ABAQUS and SAP2000, report accuracy levels nearing 95% for various structural collapse predictions. Incremental loading is applied to the model to evaluate non-linear behavior, including plastic hinge formation and failure. Furthermore, techniques, like non-linear static or dynamic pushover analysis, are almost always used to generate realistic stress-strain relationships.
EUROCODE AND LIMIT STATE DESIGN APPROACHES
Modern codes, e.g., Eurocode, outline processes on how to estimate the partial safety factor collapse load factor. Eurocode 3 squeezes within imperfection provisions for steel structures while Eurocode 8 expands onto temporal sequential collapse design enabling design goals to control progressive collapse.
LIMIT STATE DESIGN
Scaled models of structures are tested under controlled conditions to measure failure mechanisms for validation of collapse load calculations. For example, recent research exposed that reinforced concrete beams under increasing load exhibits predictable behavior, with a leveling error of 5-10%.
Integration of Machine Learning and AI Technologies
As technology increases, AI-based approaches for predicting collapse loads estimation are becoming more common. Machine learning models are developed on the foundation of vast experimental and simulated datasets, enabling quicker and more precise evaluations of models. Google AI recently announced advances in predicting the structural collapse loads using neural network models.
Data Relevant to the Collapse Load Factor Analysis
Steel Frame Example
A recent publication in the “Journal of Structural Engineering” indicated that FEA could estimate the collapse load factor of a multi-story steel frame structure with an accuracy range of 3% of the experimentally determined value.
High-Rise Buildings Under Seismic Loads
Studies on high-rise buildings subjected to simulated seismic activity showed that the use of pushover analysis in conjunction with the Eurocode guidance resulted in improved accuracy for predicting the seismic collapse loads by almost 20% from previous estimates.
The integration of these techniques, alongside the progress in technology, plays a pivotal role in improving the efficiency and trustworthiness of the calculations for the collapse load factor and designing more precise and dependable structures.
What are the Challenges in Using Plastic Analysis?
While plastic analysis remains effective in examining the behavior of structures, it has various outlines. One such example is its reliance on defining material properties that are ideal and homogeneous. This creates a challenge when a material has anisotropy and various imperfections are present. Moreover, the methodology demands exhaustive information about the control loads and collapse mechanisms which are often very difficult to obtain for complex structures. Additionally, dynamic loads, sudden forces, and even unaccounted external impacts tend to be approximated in a far too simplistic manner. This weakens the credibility of the assumptions. Overall, the amount of knowledge required is excessive due to factors such as erroneous assumptions, inaccuracies, and misleading conclusions, resulting in a multitude of unsafe designs.
Dealing with Elastic-Perfectly Plastic Behavior
Elastic-perfectly plastic behavior is an important term in material science and structural engineering which refers to the reaction of materials when force is applied. In the beginning, a material behaves elastically, which means it deforms in response to stress and gets back to its original form once the stress is released. Nevertheless, after crossing the yield point of stress, the material enters the plastic phase where constant deformation will occur with no change in stress will be added.
To make a correct model and analyze this behavior, the following points are important to consider:
Key Features:
Material properties: Exact attributes with regards to yield strength, ultimate strength, and modulus of elasticity require precise determination. For example, in structural engineering, steel is a common choice because of its yield strength and it’s elastic-perfectly plastic response. Nowadays tools allow refinement of these characteristics using experimental data.
Stress-Strain relationship: The FEA (Finite Element Analysis) approach gives high level computational models which simulate different cases of loading on the elastic-perfectly plastic behavior. These models also have associated strain – stress curves to guarantee accuracy of predictions.
Applications in design: Design-oriented models for safety-tolerant structures are extremely important. For them, predicting the amount of load a structure can support before collapsing has to be well understood in terms of reliability. A case of this application is in steel reinforcement for use in earthquake engineering where incorporating plastic deformation into the design, along with other mitigations preserve structures from destruction under massive forces.
Theoretical Validation: Advanced simulations, as well as physical methods like tensile and bend testing, have been used to validate composite materials’ straining predictions. Graphical results often illustrate very well the regions of elastic and plastic response.
These concepts have recently been subject to more in-depth study. For instance, a 2023 paper published in Materials Science and Engineering discusses methodologies for simulating elastic-perfectly plastic deformation of composites. Moreover, the application of machine learning is now allowing more efficient analysis of datasets to predict material responses.
Theoretical knowledge paired with experimental techniques and modern technologies helps engineers design systems that withstand elastic-perfectly plastic behavior while ensuring safety and functionality in real-world scenarios.
Ensuring Sufficient Plastic Hinges in Structures
In ductile structures, especially in seismic resisting systems, the importance of plastic hinges cannot be overemphasized. Passive energy systems and under structural control systems allow for the damping of energy through controlled plastic deformation during extreme loads, like earthquakes. The engineer, in order to achieve specific plastic hinges, needs to consider the geometry of the structure, material, and detailing of reinforcements.
There appears to be an increased reliance on performance-based frameworks that utilize a range of nonlinear dynamic analyses to evaluate hinges and their behavior under cyclic loading, marking an important step in contemporary research on plastic hinges. Research states that for optimal energy dissipation, control of plastic hinges in beams and columns must be placed and spaced adequately.
It is also indicated that novel materials like high-strength steel and fiber-reinforced polymers have quite a positive impact on the behavior of a plastic hinge. For instance, high-strength steel serves to increase the load-bearing capacity while the polymer gives further confinement of the concrete within hinges which enhances ductility. Several case studies conducted recently portray a considerable increase of 25-30% in the total amount of damping the structure offers during seismic activity when applying modern materials.
Moreover, the emerging features of tools such as finite element analysis software require high precision in modeling plastic hinge behavior. Software like ABAQUS and SAP2000 enables engineers to model multiple loading conditions and identify likely failure regions, reinforcing that adequate hinge mechanisms are added to the designs.
Incorporating the use of modern materials and computational modeling, along with the use of traditional principles, poses the ability to construct design meeting the rigorous safety while balancing costs, resources, and performance.
Addressing Collapse Mechanism Complexity
A merge between theoretical understanding, real-world experience, and advanced computation techniques is needed when examining structures in the context of collapse mechanisms. The strides made in computational modeling in recent years have allowed for improved analysis of complex systems. As per academic sources like Google Scholar and other recent research publications, tools such as Finite Element Analysis (FEA) have aided in determining progressive collapse scenarios in structures. These tools enable speculations regarding changes in stress distribution and broken conditions, which are very useful to engineers.
Studies equally recognize the impact of material and joint detailing behavior alongside structural failure. The use of advanced concrete high in strength, also referred to as ultra-high-performance concrete (UHPC), is on the rise to counter localized failure mechanisms. As per some freshly conducted experiments, the application of UHPC has the potential to lower brittle cracking by around thirty percent relative to conventional concrete, as published in some engineering journals.
Another essential aspect of controlling risk is the redundancy designs. Recently developed computational algorithms are capable of optimizing the alternate load paths to avert collapse and guarantee survival to localized failure. A recent case study on a high-rise building showed that strategically adding bracing elements cut the risk of collapse by 45%, setting a standard for contemporary structural design.
Contemporary engineering solutions draw upon the innovations of modern materials, sophisticated computing, and rigorous failure evaluation to tackle the challenges posed by structural collapse more effectively than ever before. This collaboration guarantees enhanced safety without imposing heavy financial burdens.
Reference Sources
- Classroom Analysis of Various Plastics
This study focuses on the properties of different plastics and their analysis through active learning techniques.
- Designing an Educational Website Regarding the Recycling of Plastic Waste into Roads
This paper elaborates on plastic waste examination and its potential use as a road construction material.
- An Analysis of a Waste Audit Performed on UNL Campus Buildings
This research consists of classifying and examining both qualitative and quantitative aspects of plastics in waste audit samples.
Frequently Asked Questions (FAQs)
Q: What is plastic analysis in structural engineering?
A: Plastic analysis is a method in structural engineering that involves determining the load-carrying capacity of structures by considering the plastic behavior of materials. It focuses on the redistribution of internal forces and the formation of plastic hinges until a collapse mechanism is formed, allowing for an assessment of the ultimate strength.
Q: What are the main methods of plastic analysis?
A: The main methods of plastic analysis include the mechanism method, the equilibrium method, and the method of plastic moment distribution. These methods help in calculating the collapse load and load factor for structures like beams and frames.
Q: How does plastic analysis differ from elastic analysis?
A: Plastic analysis considers the inelastic behavior and plastic moment capacity of materials, allowing for redistribution of stresses beyond the elastic limit. Elastic analysis, on the other hand, assumes that materials remain within their elastic range and do not account for plastic hinge formation or collapse mechanisms.
Q: What is a plastic hinge, and why is it important in plastic analysis?
A: A plastic hinge is a localized zone in a structural member where plastic deformation occurs, allowing rotation without an increase in moment. It is crucial in plastic analysis because the formation of sufficient plastic hinges can lead to a collapse mechanism, helping to determine the structure’s load capacity.
Q: What is the significance of the load factor in plastic analysis?
A: The load factor in plastic analysis is the ratio of the collapse load to the actual applied load. It is significant because it indicates the safety margin of a structure, with a higher load factor suggesting greater safety.
Q: How is the method used in the plastic analysis of beams?
A: The mechanism method involves assuming possible collapse mechanisms and calculating the corresponding collapse load using principles of virtual work and kinematic compatibility. This method helps in determining the actual collapse load and verifying the sufficiency of plastic hinges.
Q: What role do theorems play in plastic analysis?
A: Theorems such as the upper bound theorem and lower bound theorem provide foundational principles for plastic analysis. They help in establishing the conditions for collapse and ensuring that the calculated plastic collapse load is either a safe approximation or the exact load-carrying capacity.
Q: How is plastic analysis applied in the design of steel structures?
A: Plastic analysis is used in the design of steel structures to optimize material use by allowing for the redistribution of moments and forces. It helps in designing structures that can withstand loads beyond the elastic limit, ensuring safety and efficiency.
Q: Can plastic analysis be used for statically indeterminate structures?
A: Yes, plastic analysis can be effectively used for statically indeterminate structures. It allows for the consideration of plastic hinge formation and redistribution of internal forces, enabling the determination of the ultimate load-carrying capacity of complex structural systems.






